アルバイト・パート賃金相場は平均値だけでは読み取れない?
人と仕事研究所では、アイデムの発行している新聞折り込み広告「しごと情報アイデム」の紙面から、募集時の賃金データを収集しています。収集した結果から、パート・アルバイトの時給データを抽出・集計し、毎月「パートタイマーの募集時平均時給」として公表したり、年1回冊子に製本して、お客様にお役立ち資料として活用していただいております。
また、人と仕事研究所のWEBサイト内の「平均時給検索システム」も、紙面から収集した情報を元にしています。今回のオリジナル調査では、「パートタイマーの募集時平均時給」の結果表を元に、それぞれの項目の意味やそこから読み取れることをご紹介いたします。
東日本エリア(東京都、神奈川県、埼玉県、千葉県、茨城県、群馬県、栃木県、静岡県)
職種大分類集計
| 大分類 | パート・アルバイトの募集時時給(円) | 対前年同月比較 | |||||
|---|---|---|---|---|---|---|---|
| 25%ile | 50%ile | 75%ile | 最頻値 | 平均値 | 増減額(円) | 増減率(%) | |
| 専門・技術職 | 940 | 1,100 | 1,500 | 1,000 | 1,285 | 37 | 3.0 |
| 事務職 | 850 | 910 | 980 | 1,000 | 926 | 20 | 2.2 |
| 販売・営業職 | 850 | 910 | 970 | 910 | 929 | 17 | 1.9 |
| フード・サービス職 | 840 | 900 | 950 | 850 | 906 | 13 | 1.5 |
| 運輸・通信・保安職 | 900 | 1,000 | 1,100 | 1,000 | 999 | 13 | 1.3 |
| 製造・建設・労務職 | 850 | 910 | 1,000 | 1,000 | 939 | 18 | 2.0 |
| その他 | 800 | 820 | 900 | 820 | 858 | -3 | -0.3 |
| 全体計 | 850 | 910 | 1,000 | 1,000 | 986 | 12 | 1.2 |
参考:パートタイマーの募集平均時給~平成27年11月集計結果
上の表は「パートタイマーの募集時平均時給」に掲載している集計の一つです。職種を大まかに分類した「職種大分類」の集計結果と前年同月の平均時給との比較をまとめています。
●25%ile、50%ile、75%ile :データを小さい順に並べたときに、小さいほうから1/4のところにあるデータを25%ile(第1四分位数)、1/2のところにあるデータを50%ile(第2四分位数、中央値)、3/4のところにあるデータを75%ile(第3四分位数)といい、まとめて四分位数(四分位値)といいます。
“%ile”は「パーセンタイル」と読みます。集団に含まれるデータの分布を把握するときに役立ちます。
●最頻値:集団の中で、最も度数(頻度)の多い値を示す言葉です。
●平均値:集団に含まれる全てのデータを足して、それをデータの個数で割った値です。代表の値としてよく使われています。
●増減額(円)、増減率(%):当年当月(上記表でいえば平成27年11月)の平均値が、前年同月(上記表でいえば平成26年11月)の平均値と比べてどれだけ変化したかを表しています。
参考になるのは平均値?
「内定を保有している学生一人あたりの内定獲得者数は平均で2.5社」「平成27年平均有効求人倍率は1.20倍」など、調査や集計の結果で使う代表の値として、平均値(相加平均)があります。
「パートタイマーの募集時平均時給」でも、平均値を使っています。平均値は「全てのデータを足して、それをデータの個数で割る」ことで求められるため、容易に算出することができ、かつこの容易さから相手に伝えやすいという特徴があります。
その一方で、平均値は「外れ値」の影響を受けやすいという特徴があります。外れ値とは、その集団の中で極端に値が高かったり、逆に低かったりするデータを指します。
外れ値の含まれる集団の平均値からは、実情を把握しきれないことがありますので、注意が必要です。
特に賃金に関する情報では、平均値だけでなく、最頻値や四分位数にも目を向けていただくと、実際の募集がよりイメージしやすくなります。
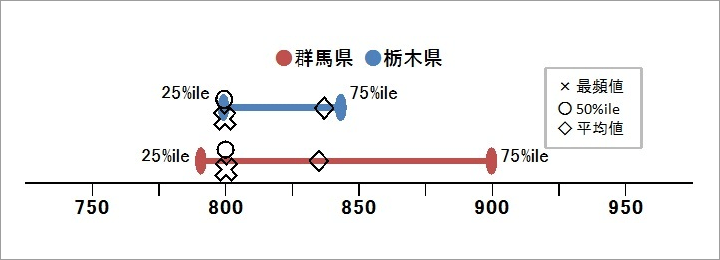
次の表は、「パートタイマーの募集時平均時給」の内容の一部を抜粋したものです。群馬県と栃木県の事務職の時給を比較しています。
| 事務職 | パート・アルバイトの募集時時給(円) | ||||
|---|---|---|---|---|---|
| 25%ile | 50%ile | 75%ile | 最頻値 | 平均値 | |
| 群馬県 | 790 | 800 | 900 | 800 | 833 |
| 栃木県 | 800 | 800 | 840 | 800 | 837 |
群馬県の事務職の平均時給は833円、栃木県は837円です。群馬県の事務職の最頻時給は800円、栃木県も800円です。平均値と最頻値から考えると、「大体同じくらいの時給の募集が多いかな」という印象を受けやすいと感じます。
しかし、四分位数に目を向けると、そうとも言い切れないことが分かります。
前述の通り、四分位数は「母集団に含まれるデータの分布を把握」したいときに役に立ちます。そして、外れ値の影響はあまり受けないのが特徴です。
今回の表では、50パーセンタイルは群馬県・栃木県ともに800円ですが、25パーセンタイルと75パーセンタイルの値は異なっています。25パーセンタイルはそれぞれ、群馬県では790円、栃木県では800円です。
75パーセンタイルはそれぞれ、群馬県では900円、栃木県では840円です。これらの値から、群馬県と栃木県の事務の募集が、それぞれどのくらい幅広くあるのかをイメージできます。
たとえ平均値や最頻値が近い数値を表していても、四分位数が異なる場合は、図のように大きく分布が異なることがあります。今回の場合、群馬県と栃木県で大きく差がある部分は、平均値から75パーセンタイルの部分です。
平均値は外れ値の影響を受けやすいので、栃木県は「75パーセンタイルの範囲より高い時給の募集がある程度あったのかな」と考えられるほか、データの散らばりが群馬県より小さいことがわかります。
75パーセンタイルの値から25パーセンタイルの値を引いた数値を、一般的に「四分位範囲」といいます。四分位範囲が大きいと、データの散らばりが大きく、上の図の群馬県のようになります。四分位範囲が小さいと、上の図の栃木県のようになります。
賃金相場で考えると、幅広い募集時給がある場合は四分位範囲が大きく、募集時の時給がある値の前後に密集している場合は、四分位範囲が小さくなります。
最近では、都道府県や職種によって、四分位範囲が小さくなることがあります。特に都心部では郊外に比べ、その傾向がより出ています。次の表は、「パートタイマーの募集時平均時給」の内容の一部を抜粋したもので、運輸・通信・保安職の東京都・神奈川県・埼玉県・千葉県・茨城県の募集時時給の情報です。
| 運輸・通信・保安職 | パート・アルバイトの募集時時給(円) | |||||
|---|---|---|---|---|---|---|
| 25%ile | 50%ile | 75%ile | 最頻値 | 平均値 | 四分位範囲 | |
| 東京都 | 920 | 1000 | 1000 | 1000 | 1008 | 80 |
| 神奈川県 | 920 | 1000 | 1000 | 1000 | 1022 | 80 |
| 埼玉県 | 900 | 950 | 1000 | 1000 | 951 | 100 |
| 千葉県 | 900 | 1000 | 1150 | 1000 | 1036 | 250 |
| 茨城県 | 850 | 1000 | 1200 | 1200 | 1027 | 350 |
茨城県を除く都県では、最頻値が1,000円です。平均値は950円から1,040円の間となっています。
四分位数と四分位範囲を見てみます。すると、東京都と神奈川県は全く同じ値で、茨城県は四分位範囲が最も大きくなっています。東京都・神奈川県の四分位範囲は80、茨城県は350です。
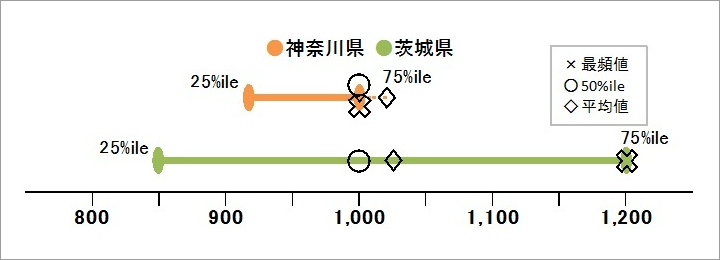
下に神奈川県と茨城県の分布イメージ図を掲載しています。神奈川県については、50パーセンタイル・75パーセンタイル・最頻値が1,000円ということと、平均値もそれに近い値をとっているので、かなりの募集が時給1,000円で設定されていると考えられます。
一方、茨城県については、四分位数がそれぞれ離れていることから、募集時の時給にはかなりばらつきがあると考えられます。また、最頻値が1,200円と高いのに平均値は1,027円というところから、1,000円から1,200円の間での募集はあまり多くないのでは、とも考えられます。
都心部で四分位範囲が小さくなるのには、どの企業でも「同じ時給」での募集が多くなっていった結果ではと考えられます。都心部であれば交通機関がかなり細かく利用できるので、求職者はより条件の良い案件に流れてしまうからです。
このように、平均値のみに頼るのではなく、最頻値や四分位数にも目を向けることで、より一層実情にあった賃金の把握に繋げることができます。
ここまで「平均以外の情報を合わせて見て」と述べてきましたが、平均値のみに注目したほうが分かりやすいこともあります。特に時系列変化をみる場合では、外れ値や季節による多少の変動があったとしても、傾向が読み取りやすいためです。「今募集をかけたい」「パートさんの賃金の見直しを図りたい」場合には、平均時給のほかにも、今回紹介しました四分位数や最頻値も併せて参考にしてみてください。